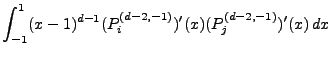1. High Order Finite Elements

Basis functions minimizing the condition number.
In [1] the construction of basis functions minimizing the iteration number is described. The resulting shape functions $\varphi_i$ are compositions of certain orthogonal polynomials involving integration and linear combinations. Using his symbolic summation package Sigma [11] C. Schneider derived recurrence relations allowing an efficient computation of the functions $\varphi_i$ .

Inner shape functions using integrated Jacobi polynomials.
In [2] shape functions for triangular -FEM are described which are constructed using products of specific Jacobi polynomials $P_n^{(\alpha,\beta)}.$ The parameters $\alpha,\ \beta$ are chosen to obtain a sparse system matrix in the case of a constant coefficient function and a polygonally bounded domain. For the case of a curved domain or a non constant coefficient function an efficient preconditioner is derived.
The idea of this design was carried over to tetrahedral finite elements. To obtain the correct parameters $\alpha,\ \beta$ in the definition of the basis functions and especially to prove the sparsity of the system matrix, the assistance of computer algebra software was needed.
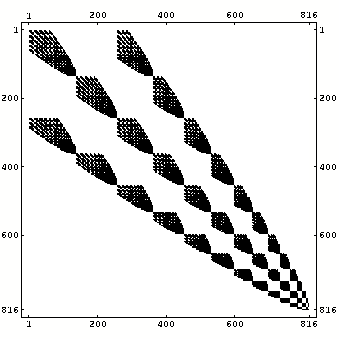
With a Mathematica program we proved the nonzero pattern of the interior block of the system matrix, i.e.,
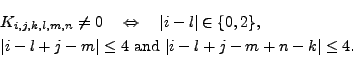
$\begin{multline*} K_{i,j,k,l,m,n} \ne 0 \quad \Leftrightarrow \quad \vert i-l\v... ...-l+j-m\vert \le 4 \ \textrm{and} \ \vert i-l+j-m+n-k\vert \le 4. \end{multline*}$
Currently we are investigating the numerical properties of these basis functions as well as the construction of an efficient preconditioner for the system matrix.

**Figure 1:** Nonzero pattern of the system matrix

A Mathematica FEM package.
In order to have a platform for numerical-symbolic interaction V. Pillwein developed the Mathematica package Fem2D. Within this program the RISC symbolic summation package (including Sigma, MultiSum, ...) can be invoked directly.

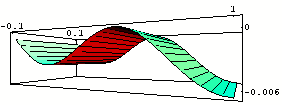
Orthogonal polynomials, which are widely used in the design of fe-basis functions, can be represented in different ways such as using their recursive description or hypergeometric sum representation. In a symbolic framework one can exploit this variety and study the benefits of different representations.

In the example described above, carefully chosen Jacobi polynomials were used in the construction of new shape functions. The Mathematica FEM package allows to generalize this idea to a systematic application of CA in the designing process. In Fem2D it is possible to implement families of basis functions leaving some parameters unknown, which are later specified according to desired numerical properties.

**Figure 2:** Elastic beam (solution by `Fem2D`)

2. Symbolic Integration of Special Functions

The particular need within F1301 for a symbolic integration algorithm that can do definite integrals arising in connection with high order finite element methods such as

$\displaystyle \int_{-1}^1 (x-1)^{d-1} (P_{i}^{(d-2,-1)})'(x)(P_{j}^{(d-2,-1)})'(x) \, d x$

(1)

involving Jacobi polynomials $P_n^{(\alpha,\beta)}(x)$ led B. Zimmermann to a new symbolic algorithm for doing definite integrals of a large class of special functions that depend on a discrete parameter.

A function is called elementary if it is obtained by composing exponentials, logarithms, algebraic functions, and field operations. Risch gave a complete algorithm for the symbolic integration of elementary functions. Given an elementary function , it decides if an elementary function exists such that . If such a exists, it returns it. Note that Risch's algorithm does not apply to integrals such as (1) for two reasons. First, the Jacobi polynomials $P_n^{(\alpha,\beta)}(x)$ appearing in (1) are not elementary (when is undetermined); in fact, most of the classical special functions from mathematical physics are not elementary. Second, Risch's algorithm is restricted to indefinite integration problems, while (1) is definite.

A recent algorithm that applies to a wide class of non-elementary special functions is Manuel Bronstein's Poor Man's Integrator [3]. It is a variant of Risch-Norman's parallel integration method, based on a new structure theorem of Manuel Bronstein.

Within the frame of F1301, B. Zimmermann extended Bronstein's Poor Man's Integrator to definite integration problems where the integrand depends on a discrete parameter . Given such an integrand and a natural number , his algorithm looks for coefficients $c_0(n), c_1(n), \dots, c_r(n)$ and a function such that

$\displaystyle c_0(n) f(x;n) + \dots + c_r(n) f(x;n+r) = g'(x;n);$

this relation implies the linear recurrence

$\displaystyle c_0(n) s(n) + \dots + c_r(n) s(n+r) = g(b;n) - g(a;n)$

for the definite integral $s(n) := \int_a^b f(x;n) dx$ under consideration.

Zimmermann's extension of the Poor Man's Integrator is inspired by Doron Zeilberger's extension of Gosper's algorithm for hypergeometric summation (Zeilberger's algorithm). The same method was used by C. Schneider [11] in his extension of Karr's summation algorithm to definite summation. In all three cases, the key is to observe that the underlying algorithm has the special property that it can be applied to an input $f(x;n) := c_0(n) f_0(x;n) + \dots + c_r(n) f_r(x;n)$ , where , ..., are initially undetermined coefficients and , ..., are given. These coefficients show up as additional variables in the linear equation system which the underlying algorithm solves. That way, the underlying algorithm determines them, in addition to determining a suitable such that . To find recurrences for integrals, one uses this with for $i=0,\dots,r$ .

The new algorithm works in a field of of rational functions $F = K(X_{u+1},\dots,X_{u+v})$ where $K = k(X_1, \dots, X_u)$ with a field. is endowed with a shift $\sigma$ and a derivation , which commute with each other, and such that the field of constants of is and that is in the field of constants of $\sigma$ . Each indeterminate corresponds to some term which possibly involves and , the shift $\sigma$ corresponds to the shift $n\mapsto n+1$ , and the derivation corresponds to the partial derivative $\frac{\partial}{\partial x}$ . For any P-finite function one can construct such a suitable field which models the field of functions generated by all the shift-derivatives of . Given $f_1, \dots, f_r$ in , the new algorithm returns a basis for the -vector space of all $(c_1, \dots, c_r,g) \in K\times F'$ such that $c_{1} f_{1} + \dots + c_{r} f_{r} = g$ and is an elementary extension of the differential field . As the algorithm is based on Bronstein's heuristic Poor Man's Integrator, it may, in rare occasions, return a basis for a proper subspace of this -vector space.

So far, the best computer algebra methods for definite symbolic integration of special functions were based on elimination in Ore Algebras by Gröbner basis methods (e.g. [4])). These methods are restricted to P-finite integrands, and they are known to terminate for the class of holonomic integrands, which form a subclass of the class of P-finite integrands. While Zimmermann's extension also handles any P-finite integrand and terminates on holonomic input, it can handle a wider class of inputs. The class of inputs which it can handle is closed under composition - unlike the class of P-finite functions. It contains certain non-P-finite functions such as the tangent function and Lambert's function.

The new algorithm is not yet published; it will appear in a forthcoming Ph.D. thesis [13].

3. Applications of Gröbner Bases

3.1 Implementations of Gröbner Bases

In the algebraic treatment of systems of equations involving linear operators (like partial differentiation, partial difference and so on), the choice of coefficient domain leads us to different algebraic structures. For the case of constant (scalar) coefficients, the underlying system algebra is commutative. If the coefficients are polynomial in the variables of the system, we obtain a non-commutative -algebra (e.g. [8]). Numerous algorithms, based on Gröbner bases for these two cases, are implemented in the specialized Computer Algebra System SINGULAR [7]. The system is freely available for the non-commercial use and, moreover, is widely known for its performance. In 2004, the SINGULAR team was awarded with the Richard D. Jenks Memorial Prize for Excellence in Software Engineering for Computer Algebra. The non-commutative subsystem SINGULAR:PLURAL [6] handles the algebras arising from systems with polynomial coefficients, including algebras with additional polynomial identities. For example, the algebra of linear differential operators with polynomial coefficients in trigonometric functions is realized as a factor algebra. Let be the algebra generated by $\{sin, cos, \d\}$ over ${\mathbb{K}}$ subject to the relations $\d\cdot sin = sin \cdot \d + cos$ , $\d\cdot cos = cos \cdot \d -sin$ and $sin \cdot cos = cos \cdot sin$ . Then, we consider the two-sided ideal $T = \langle sin^2+cos^2-1 \rangle \subset A$ , compute its two-sided Gröbner basis (which is just $\{sin^2+cos^2-1\}$ in this case) and pass to the factor algebra , where the further computations will take place.

Generalization of Gröbner Bases.
In order to treat the case of rational functions in the variables as the coefficient domain, we employ the notion of an Ore localization. Our aims are to extend the Gröbner bases theory to the Ore-localized -algebras, not restricting ourselves to the case of so-called Ore algebras ([4], [5]), to investigate the criteria for discarding the critical pairs and to implement efficiently Gröbner bases and related algorithms (involving advanced ones as in e.g. [8]) in the framework of SINGULAR. One of the most important tasks is to provide powerful algorithms and their efficient implementation for the complicated arithmetics over rings of quotients of non-commutative domains.

Intercommunication packages.
With the help of recent packages, the fast and functionally rich implementation of algorithms, relying on Gröbner bases in SINGULAR, became available to the general purpose systems. The package, allowing MATHEMATICA to exchange data and to call SINGULAR externally, is being developed by Manuel Kauers, F1305.

3.2 Symbolic Generation and Stability Analysis of Finite Difference Schemes

For the linear PDEs with constant coefficients the process of generating finite difference schemes may be performed symbolically, with the help of Gröbner bases for submodules of free modules over a commutative polynomial ring. We propose a more efficient method than the one proposed in [12]. Our method can be applied, in particular, for higher spatial dimensions without significant loss of performance. It can be shown that applying several symbolic approaches we are able to reproduce all the classical finite difference schemes. The input data consist of equations and corresponding approximation rules for the partial derivatives, written in terms of polynomials in partial difference operators like , where $T_x \bullet u(x_j,t_n) = u(x_{j+1},t_n)$ for discrete indices .

For the equation $u_{tt} - \lambda^2 u_{xx}=0$ with some initial conditions, we apply the 2nd order central approximations for both and in the vector operator form, e. g. $(- {\triangle}x^2 \cdot T_x, \; (1-T_x)^2) \bullet (u_{xx}, u)^T = 0$ . With this symbolic data we form a submodule of a free module involving partial difference operators. By using Gröbner bases, we eliminate certain module components from a given module and obtain a submodule, corresponding to the operators, which depend only on and not on its derivatives.

We denote $d:= \lambda {\triangle}t / {\triangle}h$ , and obtain the scheme, written in terms of operators,

$\displaystyle d^2 T_x^2 T_t-T_x T_t^2 +(-2 d^2+2)T_x T_t-T_x+d^2 T_t = 0.$

Using specially developed visualization tools (e. g. a SINGULAR library discretize.lib), in a semi-automatic way we are able to present the scheme above in the more convenient nodal form, namely as

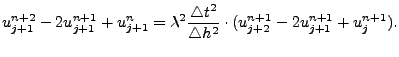
$\displaystyle u^{n+2}_{j+1}-2 u^{n+1}_{j+1}+u^{n}_{j+1} = \lambda^{2} \frac{{\t... ...le}t^{2}}{ {\triangle}h^{2}}\cdot (u^{n+1}_{j+2}-2 u^{n+1}_{j+1}+u^{n+1}_{j}).$

With our methods we are able to generate all the classical linear schemes (as it has been noted in [12]) as well as more complicated schemes, including the schemes with parametric switches.

Using the efficient implementation of Gröbner bases, these 1-dimensional examples both in time and space can be computed in seconds.

Von Neumann Stability Analysis.
Also, the investigation of von Neumann stability of a given finite difference scheme can be done by symbolic methods. Moreover, for (un-)conditionally stable schemes we can perform the dispersion analysis. For both applications the system SINGULAR is used for polynomial computations, mappings and the translation of the output to the special (nodal) form, used in the literature on finite difference schemes. MATHEMATICA is used for computing the Cylindrical Algebraic Decomposition, arising in the final stage of both stability and dispersion analysis.

In the example above, we employ the stability morphism from the ring $R={\mathbb{K}}(d)[T_x,T_t]$ , sending $T_t \mapsto g$ and $T_x \mapsto sin + i \cdot cos$ to the ring $S = {\mathbb{K}}(d)[i,sin,cos,g]/$ $/\langle sin^2+cos^2-1, i^2+1\rangle$ . Here, $sin = \sin(\alpha), cos = \cos(\alpha)$ and $\alpha = \beta {\triangle}x$ for some $\beta$ . After the purely algebraic simplification in the ring , we obtain the stability polynomial in one variable , where $b:=-1+2d^2 \sin^2(\alpha/2)$ . A scheme given by a polynomial in one variable is von Neumann stable, if the modulus of every root is at most 1. In our example, the stability polynomial has roots $b\pm\sqrt{b^2-1}$ . If , the absolute value of one of the roots is bigger than one. If $b^2\leq 1$ , the modulus of both roots is equal to 1. Moreover, $b^2\leq 1 \Leftrightarrow d\leq 1$ . Hence, the investigated scheme is conditionally stable with the condition for the Courant number $d=\lambda {\triangle}t / {\triangle}h \; \leq 1$ .

We are going to apply the developed methods for finite difference schemes in cases of higher spatial dimensions, for systems of multidimensional equations, for two-step schemes like Lax-Wendroff etc.

A very important direction of further research (discussed with Prof. W. Zulehner, F1306) is to elaborate the conditions for boundary value problems, for which von Neumann stability (which can be checked by symbolic methods as we have sketched above) implies the numerical stability.

3.3 Control Theory

Algebraic Analysis.
Given a module over an algebra , we can present it as a sum , where is a torsion submodule of and a torsion-free submodule. In Control Theory, there is a correspondence between this presentation and the decomposition of a system into a controllable part (torsion-free submodule) and an autonomous part (torsion submodule). For systems of equations, involving linear operators, the torsion submodule can be described and computed with the help of homological algebra [5], which in turn depend heavily (both algorithmically and in the implementation) on Gröbner bases.

The methods of algebraic analysis, applied to the problems of Control Theory, have been implemented for the case of constant coefficients [9] in the library control.lib for the system SINGULAR [7]. The development of the generalization to the case of variable coefficients is in progress. It relies on the implementation of Gröbner bases in the system SINGULAR:PLURAL [6] and on the library for non-commutative homological algebra.

Genericity of Parameters.
In systems, containing parameters, it often happens that some structural properties, like controllability or autonomy, hold only for the generic case, that is, for almost all values of parameters. It means, there might exist such values of parameters that, e.g. a generically controllable system, specialized at these values, becomes non-controllable. We provide an algorithmic way to detect such and similar phenomena, which we call the genericity violation. The results for 1-dimensional systems appear in [10], while in the future we concentrate on the general situation.

Bibliography

1: A. BECIROVIC, P. PAULE, V. PILLWEIN, A. RIESE, C. SCHNEIDER, AND J. SCHÖBERL.
Hypergeometric Summation Methods for High Order Finite Elements.
Tech. Rep. 2006-8, SFB F013, J. Kepler University Linz, 2006.
2: BEUCHLER, S., AND SCHÖBERL, J.
New shape functions for triangular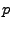 -FEM using integrated Jacobi polynomials.
Num. Mathematik (2006).
to appear.
3: BRONSTEIN, M.
Symbolic Integration I (Transcendental Functions), 2nd ed.
Springer, 2005.
4: CHYZAK, F. AND SALVY, B.
Non-commutative Elimination in Ore Algebras Proves Multivariate Identities.
J. Symbolic Computation 26, 2 (1998), 187-227.
5: CHYZAK, F., QUADRAT, A. AND ROBERTZ, D.
Linear control systems over Ore algebras. Effective algorithms for the computation of parametrizations.
In Proc. TDS'03 (2003), INRIA.
6: GREUEL, G.-M., LEVANDOVSKYY, V., AND SCHÖNEMANN H.
PLURAL, a SINGULAR 3.0 Subsystem for Computations with Non-commutative Polynomial Algebras. University of Kaiserslautern, 2005.
7: GREUEL, G.-M., PFISTER G., AND SCHÖNEMANN H.
SINGULAR 3.0. A Computer Algebra System for Polynomial Computations. Centre for Computer Algebra, University of Kaiserslautern, 2005.
Available from http://www.singular.uni-kl.de.
8: LEVANDOVSKYY, V.
Intersection of Ideals with Non-commutative Subalgebras.
Tech. Rep. 2006-14, SFB F013, J. Kepler University Linz, 2006.
9: LEVANDOVSKYY, V. AND ZERZ, E.
Computer algebraic methods for the structural analysis of linear control systems.
PAMM 5 (2005), 717-718.
10: LEVANDOVSKYY, V. AND ZERZ, E.
Algebraic systems theory and computer algebraic methods for some classes of linear control systems.
In Proc. MTNS'06 (2006).
to appear.
11: SCHNEIDER, C.
A new Sigma approach to multi-summation.
Advances in Applied Math. 34, 4 (2005), 740-767.
12: V. P. GERDT, Y. A. BLINKOV, AND V. V. MOZZHILKIN.
Gröbner Bases and Generation of Difference Schemes for Partial Differential Equations.
SIGMA 2 (2006), 051.
13: ZIMMERMANN, B.
Symbolic Definite Integration and Summation of Special Functions.
PhD thesis, RISC, J. Kepler University Linz, 2006.
In preparation.

Please direct your comments or eventual problem reports to webmaster.

SpezialForschungsBereich SFB F013 | Special Research Program of the FWF - Austrian Science Fund