Abstract
|
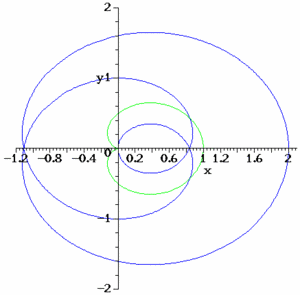
In computer aided geometric design (cagd) algebraic curves and surfaces play an essential role in modeling physical and virtual objects. The main goal of the project is the improvement and/or perfection of existing methods and the derivation of new methods for designing, manipulating, and visualizing algebraic curves and surfaces. Algebraic curves and surfaces can be represented in different ways, e.g. implicitly by a defining polynomial equation, parametrically by rational functions, or locally by Puiseux series or places. Every one of these representations has its own particular advantages, and so we need to have efficient algorithms for changing representations.
In the project we also investigate symmetries of partial differential equations, in particular 2nd order PDEs. A full classification of the symmetry groups of such a class of differential equations allows to determine many qualitative properties of the solutions.
Objectives
- real parametrization of real algebraic curves
- rational parametrization of pipe and canal surfaces
- determination of minimal surfaces
- symmetry analysis of 2nd order PDEs
People
| Prof. Dr. Franz Winkler | 9943 mail | ||
Scientific Staff
| Dr. Elena Kartaschova | 9929 | ||
| Dr. Ekaterina Shemyahova | 9950 | ||
Publications
SpezialForschungsBereich SFB F013 | Special Research Program of the FWF - Austrian Science Fund