Abstract
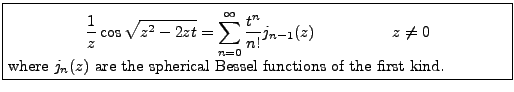
|
During the first funding period (1998-2001) the primary focus of the SFB-F1305 project work was put on symbolic summation, in particular, hypergeometric summation. In the second funding period (2001-2004), symbolic summation was considered in the more general context of difference fields. So summation still played a major role, but promising first steps toward more analysis-oriented methods, including definite integration, were made. In addition, the developed F1305 tools have been applied successfully to numerical problems, for instance, to improve high order finite element methods; a collaboration between F1305 and F1306 which is planned to be continued in the third funding period.
Highlights of the results achieved by F1305 during the second funding periods are:
- Schneider's extensions of Karr's difference field summation theory. The corresponding Mathematica package Sigma developed by Schneider was able to prove conjectured identities (related to numerical Pade approximation) that resisted serious proving attacks by human experts. A series of papers has been submitted.
- The project on partition analysis was continued very successfully (joint with G.E. Andrews). The algorithm underlying the Mathematica package Omega was thoroughly refined. Now it provides a strong problem solving tool in connection with problems of simplifying power series where the summation parameters are constrained by diophantine equations or inequalities; a series of papers with many applications was published.
- Concerning symbolic summation of hypergeometric multisums, Riese and Zimmermann achieved a remarkable break-through. By using modular techniques they were able to optimize the F1305 MultiSum algorithm developed by Wegschaider. This opens the door to a variety of special function applications, including the simplification of complicated definite integrals.
- Zimmermann's difference-differential ring algorithm, which is a new generalization of the Sister Celine/WZ method. Despite its elementary nature it is of sufficient generality to treat special function problems of various kinds and thus provides an excellent alternative to algorithms like Chyzak's. For example, it can compute suitable representations for integrals involving Legendre polynomials relevant to Schöberl's setting of high order finite elements.
- The last mentioned collaboration with F1306 (Schöberl) which already brought along remarkable speed-ups of conventional numerical methods, will be continued in an own SFB project.
Objectives
- Computer Algebra Tools for special functions
- Symbolic Summation
- Symbolic Integration
Results
Recent results of F1305 in detail.
People
| Prof. Dr. Peter Paule | 9193 mail | ||
Scientific Staff
| Dipl.-Inf. Christoph Koutschan | 9927 mail | ||
| Msc. Silviu Radu | 9981 mail | ||
Publications
SpezialForschungsBereich SFB F013 | Special Research Program of the FWF - Austrian Science Fund