The scientific output achieved in 2005 by the SFB project group F1305 is documented in the form of 21 publications: 8 articles were published in journals and 4 in conference proceedings; 9 technical reports have been produced, 4 of which are already accepted for journal publication. Additionally, two PhD-theses [9,14] have been completed.

1. Identities

Various refined summation algorithms [20,21,22,23,24,26] have been developed by Schneider that enable one to simplify and/or evaluate complicated multi-sum expressions. Examples of successful applications of these tools are: A computer proof of the "Totally symmetric plane partition" theorem [1], a quadruple sum expression that evaluates to zeta-functions [19,25], proofs of identities that are needed for Padé approximation [5,6], and the derivation of reciprocity laws of harmonic numbers that arise in the analysis of algorithms [18]. In addition, recurrences were computed that could speed up the computations in Finite Element Methods [2]; see project F1301.

Kauers and Schneider extended the summation algorithms of Schneider by allowing generic (unspecified) sequences within sums [17]. In [16] they illustrate how these algorithms can be used to discover new general identities.

In a joint effort, Paule, Gerhold, Kauers, Schneider, and Zimmermann could provide proofs of various identities in the Handbook of Mathematical Functions (Abramowitz/Stegun) whose original proofs have been lost [12]. One of of these identities is shown in the box below.

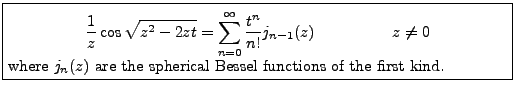
$\fbox{\parbox{.9\columnwidth}{ \begin{align*} \frac1z\cos\sqrt{z^2-2zt}&=\sum_{... ...{align*}where $j_n(z)$\ are the spherical Bessel functions of the first kind. }}$

In his Ph.D. thesis [14], Kauers presents a collection of algorithms for sequences which can be defined by nonlinear higher order difference equations. An implementation of these algorithms in form of a Mathematica package [15] is able to prove and to discover identities which were previously considered out of scope of symbolic computation. Examples include properties of Somos sequences, nested C-finite expressions, orthogonal polynomials, continued fractions, etc. A large collection of example applications is included in the thesis.

2. Inequalities and Asymptotics

Gerhold and Kauers have proposed a procedure for automatically proving inequalities among expressions that are defined via recurrence equations [10]. With this procedure, it was possible to verify a large number of inequalities appearing in the literature by a computer procedure for the first time. A remarkable example is the computer proof of Turán's inequality for Legendre polynomials [11].

Inequalities are in general harder than identities, and the procedure of Gerhold and Kauers is not able to provide a proof for every true inequality to which it is applicable. A conjectured inequality which arose in the numerical work of J. Schöberl (F1319), for example, is in the right shape for the method of Gerhold/Kauers to apply, but the method fails to supply a proof. Attempts to prove this inequality by hand using asymptotic arguments have also failed so far. See [13] for some work that has been done by Gerhold, Kauers, and Schöberl on this inequality.

In joint work with J.P. Bell [3], Gerhold has obtained a fairly satisfactory result about the sign of oscillating linear recurrence sequences: If a C-finite sequence has no real positive dominating root, then its positivity set and its negativity set both have positive density. Moreover, the density can assume each value from ]0, 1[.

3. Non-Holonomicity

Non-holonomicity results give some evidence on the algorithmic complexity of a sequence, since values of holonomic sequences can be readily computed by the linear recurrence with polynomial coefficients that defines them. Flajolet, Gerhold, and Salvy [8] have shown by an asymptotic method [7] that the sequence $\mathrm{e}^{1/n}$ is not holonomic. Along the way, amusing asymptotic results like

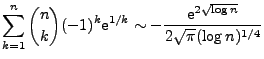
$\displaystyle \sum_{k=1}^n \binom{n}{k} (-1)^k \mathrm{e}^{1/k} \sim -\frac{\mathrm{e}^{2\sqrt{\log n}}}{2\sqrt{\pi}(\log n)^{1/4}}$

have been obtained. A completely different approach has been pursued by Bell, Gerhold, Klazar, and Luca [4]. They show how the additional structure of sequences like $\mathrm{e}^{1/n}$ and $n^{1/2}$ , which are defined by the analytic functions $\mathrm{e}^{1/z}$ and $z^{1/2}$ , can be exploited more directly to establish their non-holonomicity.

Bibliography

1: ANDREWS, G., PAULE, P., AND SCHNEIDER, C.
Plane Partitions VI: Stembridges TSPP Theorem.
Adv. in Appl. Math. 34, 4 (2005), 709-739.
2: BECIROVIC, A., PAULE, P., PILLWEIN, V., RIESE, A., SCHNEIDER, C., AND SCHÖBERL, J.
Hypergeometric summation algorithms for high order finite elements.
SFB-Report 2006-8, J. Kepler Universität, Linz, 2006.
Submitted.
3: BELL, J. P., AND GERHOLD, S.
The Positivity Set of a Recurrence Sequence.
Israel J. Math. (2005).
To appear.
4: BELL, J. P., GERHOLD, S., KLAZAR, M., AND LUCA, F.
Non-holonomicity proofs for sequences defined via elementary functions.
Submitted.
5: DRIVER, K., PRODINGER, H., SCHNEIDER, C., AND WEIDEMAN, A.
Padé approximations to the logarithm III: Alternative methods and additional results.
To appear in Ramanujan J. (2006).
6: DRIVER, K., PRODINGER, H., SCHNEIDER, C., AND WEIDEMAN, J. A. C.
Padé approximations to the logarithm II: Identities, recurrences, and symbolic computation.
Ramanujan J. 11, 2 (2006).
7: FLAJOLET, P., GERHOLD, S., AND SALVY, B.
On the non-holonomic character of logarithms, powers and the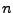 th prime function.
Electronic Journal of Combinatorics 11, 2 (2005), 1-16.
8: FLAJOLET, P., GERHOLD, S., AND SALVY, B.
Asymptotic analysis of the generating functions of certain closed form sequences.
In preparation, 2006.
9: GERHOLD, S.
Combinatorial Sequences: Non-Holonomicity and Inequalities.
PhD thesis, RISC, J. Kepler Universität, Linz, 2005.
10: GERHOLD, S., AND KAUERS, M.
A procedure for proving special function inequalities involving a discrete parameter.
In Proceedings of ISSAC'05 (2005), pp. 156-162.
11: GERHOLD, S., AND KAUERS, M.
A computer proof of Turán's inequality.
Journal of Inequalities in Pure and Applied Mathematics 7, 2 (2006).
12: GERHOLD, S., KAUERS, M., OLVER, F., PAULE, P., SCHNEIDER, C., AND ZIMMERMANN, B.
Computer proofs of some identities for bessel functions of fractional order.
In preparation, 2006.
13: GERHOLD, S., KAUERS, M., AND SCHÖBERL, J.
On a conjectured inequality for a sum of Legendre polynomials.
SFB-Report 2006-11, J. Kepler Universität, Linz, 2006.
14: KAUERS, M.
Algorithms for Nonlinear Higher Order Difference Equations.
PhD thesis, RISC, J. Kepler Universität, Linz, 2005.
15: KAUERS, M.
SumCracker -- a package for manipulating symbolic sums and related objects.
SFB-Report 2005-21, J. Kepler Universität, Linz, 2005.
Submitted.
16: KAUERS, M., AND SCHNEIDER, C.
Application of unspecified sequences in symbolic summation.
To appear in ISSAC'06 (2006).
17: KAUERS, M., AND SCHNEIDER, C.
Indefinite summation with unspecified sequences.
To appear in Discrete Math. (2006).
18: KUBA, M., PRODINGER, H., AND SCHNEIDER, C.
Generalized reciprocity laws for sums of harmonic numbers.
SFB-Report 2005-17, J. Kepler Universität, Linz, 2005.
Submitted.
19: PEMANTLE, R., AND SCHNEIDER, C.
When is 0.999... equal to 1?
To appear in Amer. Math. Monthly (2006).
20: SCHNEIDER, C.
Degree bounds to find polynomial solutions of parameterized linear difference equations in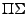 ${\Pi}{\Sigma}$ -fields.
Appl. Algebra Engrg. Comm. Comput. 16, 1 (2005), 1-32.
21: SCHNEIDER, C.
Finding telescopers with minimal depth for indefinite nested sum and product expressions.
In Proceedings of ISSAC'05 (2005), M. Kauers, Ed., ACM, pp. 285-292.
22: SCHNEIDER, C.
A new Sigma approach to multi-summation.
Adv. in Appl. Math. 34, 4 (2005), 740-767.
23: SCHNEIDER, C.
Product representations in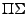 ${\Pi}{\Sigma}$ -fields.
Ann. Comb. 9, 1 (2005), 75-99.
24: SCHNEIDER, C.
Solving parameterized linear difference equations in terms of indefinite nested sums and products.
J. Differ. Equations Appl. 11, 9 (2005), 799-821.
25: SCHNEIDER, C.
Some Notes On "When is 0.999... equal to 1?".
In Mathematics, Algorithms, Proofs (2005), no. 05021 in Dagstuhl Seminar Proceedings.
26: SCHNEIDER, C.
Simplifying sums in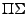 ${\Pi}{\Sigma}$ -extensions.
SFB-Report 2006-13, J. Kepler Universität, Linz, 2006.
Submitted.

Please direct your comments or eventual problem reports to webmaster.

SpezialForschungsBereich SFB F013 | Special Research Program of the FWF - Austrian Science Fund