A variety of important applications deals with the identification or optimization of shapes, whose topological structure is not known a-priori. Also parameter identification with a known finite number of parameter values but unknown distribution of parameters, can be viewed as a shape identification problem. A classical approach to optimization and identification of shapes is the parametrization approach, where one carries out optimization over the parameters representing the shape. In this case one has to know the topological structure of the shape in advance in order to construct a parametrization. While the theory of the parametrization approach is, due to its functional representation, already well developed, more flexible methods (allowing topological changes) are still in development. One such flexible method capable of topology changes, while still representing real shapes (opposed to homogenization approaches), is the level set method, based on implicit representations of the shape via functions close to the signed distance function. Though the level set method has recently been applied by several groups, there are still few rigorous theoretical results for geometrical inverse, shape and topology optimization problems. The well-posedness of the level-set evolution itself as well as its regularizing and convergence properties are not known in detail yet and hence a challenging topic of research. Furthermore, the efficient coupling of the level-set method to shape sensitivities and topological derivatives is of interest. Besides the level-set method, the closely related phase field method, originally introduced in material science as a diffuse interface model, appears to be capable of topological changes. The application of the phase field method to geometric inverse problems and topology optimization problems and the analysis of this method in terms of regularizing properties and convergence is rather open and an active research topic in this project.

 

Contact: martin.burger@jku.at or benjamin.hackl@ricam.oeaw.ac.at

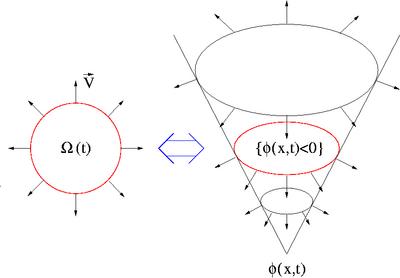The basic idea of level-set methods is to represent the domain Ω(t) as the negative sublevel set of  a function Φ(x,t),i.e.

Ω(t) = {x | Φ(x,t) < 0}.

This level set function Φ(x,t) is evolved via a special Hamilton-Jacobi equation, the so called level set equation

∂_tΦ + V_n|∇Φ| = 0,

where V_n denotes the normal velocity, and it can be shown that for smooth shapes the evolution coincides with a standard motion of the shape with normal velocity V_n on its boundary . For interface motion in physical, chemical, or biological processes, the choice of the velocity V_n is obtained from a model based on the physics of the process, whereas for geometric inverse problems and optimization problems such an velocity has to be constructed such that the value of some objective functional J(Ω(t)) decreases when t increases. This goal can be achieved using a geometric gradient flow, with gradient determined by the so-called speed method, introduced by Zolesio in the context of classical shape optimization. A main result related to shape gradients obtained by the speed method is the Hadamard-Zolesio structure theorem, which states that the
derivative is a linear functional of V_n concentrated on the boundary of Ω(t).  Under suitable regularity assumptions this yields a formula

∂_tJ(Ω(t))= ∫_∂Ω(t) V_n(t) ρ(t) ds,

where ρ(t) depends on the actual shape and the specific objective functional (in many problems
for partial differential equations it can be given in terms of the state and some adjoint state variable).

As mentioned above we want to choose the velocity V_n such that a descent in J(Ω(t)) is obtained. Assuming that V_n is in taken from a Hilbertspace X we can achieve descent in J(Ω(t)) by choosing V_n to be the unique solution of

⟨V_n,ψ⟩_X = - ∫_∂Ω(t) ψ ρ(t) ds .

The choice of a descent direction is a standard ingredient in the construction of optimization method, but it does not necessarly result into a convergent method (and indeed there are no general convergence proofs). In particular for geometric inverse problems, the choice of the Hilbert space X seems to be crucial in order to obtain a stable convergent method.

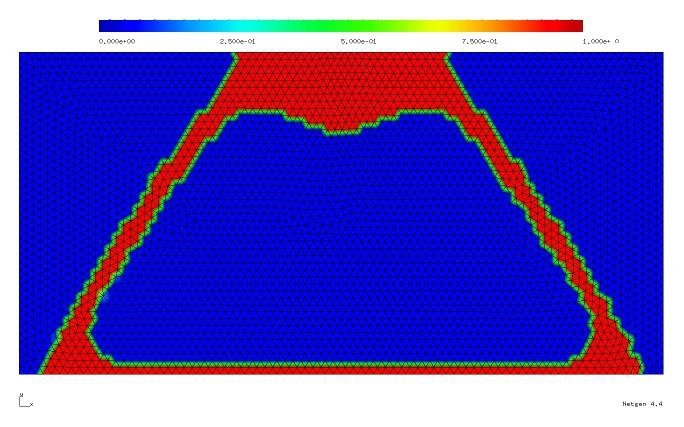
L2-update

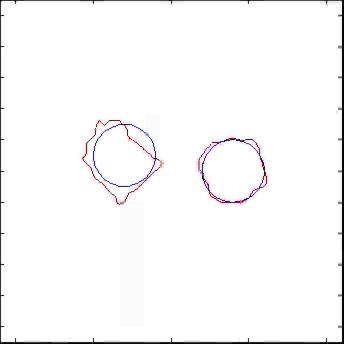
H 1/2 update

Besides the convergence issue the choice of the velocity plays also an crucial role in terms of the "convergence speed". In general, different choices of the Hilbert space X yield methods of different convergence speed. The descent method constructed above is corresponds to gradient methods in classical optimization, for which local convergence is known to be linear. In order to obtain faster local convergence, a different choice of the velocity, using second order information (like in Newton type) methods is desirable. One possibility to achieve such a fast local convergence for geometric inverse problems is to use a Levenberg-Marquardt type approach in the level set framework, which has been carried out successfully in this project.

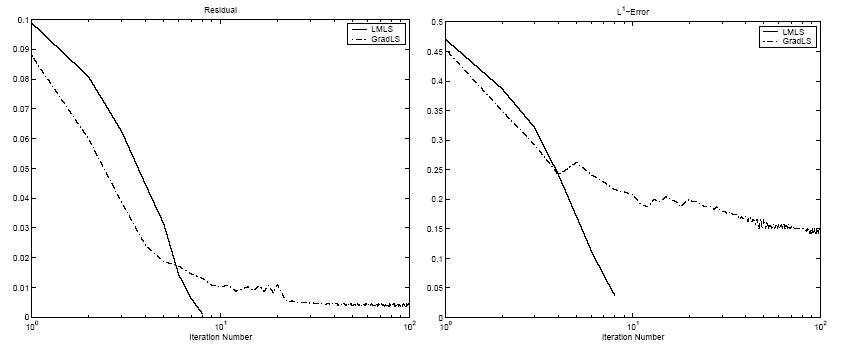
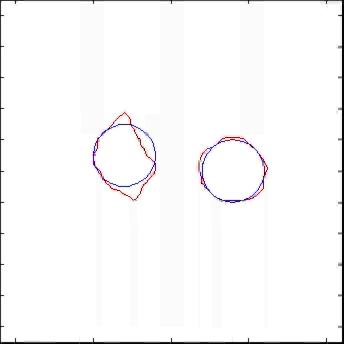
Levenberg-Marquardt vs. Speed-method

The level set method is supposed to allow topological changes but in theory and practice there are still situations of topology changes that cannot occur.
An example of particular importance are inner contours, e.g., the level set method cannot converge to a ring-type structure if the original shape is simply connected. In order to overcome this difficulty we tried to incorporate topological derivatives into the level set method. The topological derivative is given as the variation of the objective with respect to infinitesimally small nucleations, i.e. one considers

τJ(Ω)(x) := lim_ρ→0 [J(Ω−B_ρ(x))- J(Ω)] ⁄ |B_ρ| .

The limit, if it exists, can usually be computed in a similar way to shape derivatives, but it provides additional information whether it is favourable to introduce a topology change at a certain place, or not. The topology change of the level set function Φ can than either be forced by adding some additional source term to the level set equation that depends in an appropriate way on the topological derivative or by a manual nucleation and a restart of the level set equation with this additional small shape component. The idea of using additional topological derivative information in level set methods, proposed as a result of research in this project, has recently been applied to problems in structural optimization by several groups around the world.

Standard Level-Set method

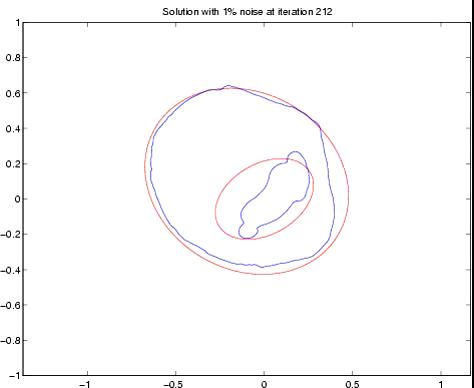
incorporating topological derivatives

• M. Burger, S. Osher, A survey on level set methods for inverse problems and optimal design, European J. Appl. Math., 2004, to appear. Preprint: .pdf
• H. Ben Ameur, M. Burger, B. Hackl, Level set methods for geometric inverse problems in linear elasticity, Inv. Prob., 20(3) 2004, 673-696. Preprint: .pdf, .ps.gz
• M. Burger, B. Hackl, W. Ring, Incorporating topological derivatives into level sets methods, J. Comp. Phys., 194(1) 2004, 334-362. Preprint: .pdf
• M. Burger, Numerical simulation of anisotropic surface diffusion with curvature-dependent energy, J. Comp. Phys. 2004, to appear. Preprint: .pdf
• M. Burger, Levenberg-Marquardt level set methods for inverse obstacle problems, Inverse Problems, 20 ,2004, 259-282. Preprint: .pdf
• B. Ben Ameur, M. Burger, B. Hackl, On some geometric inverse problems in linear elasticity, UCLA CAM-Report 03-55, 2003. Preprint: .pdf
• M. Burger, Weak solutions for the mean curvature flow of graphs, SFB-Report 03-01, 2003. Preprint: .pdf, .ps.gz
• M. Burger, A framework for the construction of level set methods for shape optimization and reconstruction, Interfaces and Free Boundaries 5, 2003, 301-329. Preprint: .pdf, .ps.gz
• M. Burger, Growth fronts of first-order Hamilton-Jacobi equations, SFB Report 02-8, 2002. Preprint: .pdf, .ps.gz
• M. Burger, A level set method for inverse problems, Inverse Problems, 17, 2001, 1327-1356. Preprint: .ps.gz

Contact: martin.burger@jku.at or stainko@sfb013.uni-linz.ac.at

The phase field method is, in contrast to the level-set method, restricted to problems where one can replace the domain Ω by the characteristic function χ_Ω. Roughly speaking, instead of a subset of D, we look for a function in the space BV(D;{0,1}). In order to detail the idea of the phase field method consider the following regularized problem

J(χ) + α Per(χ) → min_{χ∈BV(D;{0,1})} ,

where Per denotes the perimeter. In the phase field approach BV(D;{0,1}) is relaxed BV(D;[0,1]) (or even some Sobolev space with values in [0,1]), and the perimeter functional is approximated by smoother functionals. Of particular importance are Cahn-Hilliard functionals of the form

J(ψ) + ε||∇ψ||_L²(D) + 1⁄ε∫_DW(ψ) dx → min _ψ∈H¹(D),

where W is a double-well potential, e.g. W(s) = cs²(1-s)² and α=2∫₀¹ W(s)^1⁄2 ds. The convergence of the relaxed problem as ε tends to 0 can be analyzed in the framework of Γ-convergence, using the celebrated Modica-Mortola theorem. An approximate shape Ω can be reconstructed from the phase-field ψ e.g. as the level set {x | ψ > 1/2}.

For the numerical treatment of the relaxed problem all powerful tools theoretical and numerical tools for Sobolov spaces, like FEM, adaptive discretization, multigrid solvers are available. Furthermore all-at-once approaches, previously considered in this project for parameter identification, can be applied to the relaxed problem. Hence an application of the phase-field method to special classes of geometric inverse problems, and also to topology optimization problems (in cooperation with project F1309) is a topic of active research. We also try to investigate the double limit α ε tending to zero, which has not been analyzed yet.

An application of particular interest is the solution of stress-constrained topology optimization problems, where we used the phase-field method to obtain a linear relaxation of local inequality constraints. Whereas the original problem violates all common constraint qualifications, the phase-field relaxation yields a sequence of approximations with linear constraints and thus automatically satisfying constraint qualification. The relaxed problem is then solved using the interior point code IPOPT developed by Andreas Wächter.

Phase field approach

• M. Burger, R. Stainko, Phase-Field Relaxation of Topology Optimization with Local Stress Constraints SFB-Report 04-35, 2004. Preprint: .pdf, .ps.gz

Contact: martin.burger@jku.at

For severely ill-posed problems with few data, like the ones appearing in inverse scattering, there is few hope to identify objects with a complicated topological structure or with complicated shapes. Therefore, and in order to gain stability, it is favourable to use specific parametrizations for the shapes and to use iterative regularization in the space used for the parametrization. This approach has been applied with success to some problems in inverse obstacle scattering and the reconstruction of p-n junctions in semiconductor devices.

• P. Hähner,T. Hohage, New stability estimates for the inverse acoustic inhomogeneous medium problem and applications, SIAM J. Math. Anal. 33(3), 2001, 670-685. Preprint: .ps.gz
• M. Burger, H. W. Engl, P. Markowich, P. Pietra, Identification of doping profiles in semiconductor devices, Inverse Problems, 17, 2001, 1765-1795. Preprint: .ps.gz
• T. Hohage, On the numerical solution of a three-dimensional inverse medium scattering problem, Inverse Probl. 17(6), 2001, 1743-1763. Preprint: .ps.gz
• T. Hohage, Regularization of exponentially ill-posed problems, Numer. Funct. Anal. Optimization 21(3-4), 2000, 439-464. Preprint: .ps.gz
• T. Hohage, Iterative Methods in Inverse Obstacle Scattering: Regularization Theory of Linear and Nonlinear Exponentially Ill-Posed Problems, PhD thesis, University of Linz, 1999.
• T. Hohage, Iterative regularization methods in inverse scattering, In K. A. Woodbury, editor, Inverse Problems in Engineering: Theory and Practice, New York, 1999. The American Society of Mechanical Engineers. Preprint: .ps.gz
• T. Hohage, Convergence rates of a regularized Newton method in sound-hard inverse scattering, SIAM J.Numer.Anal., 36, 1998, 125-142.
• T. Hohage, C. Schormann, A Newton-type method for a transmission problem in inverse scattering, Inverse Problems, 14(5), 1998, 1207-1227.

Besides internal cooperations within the SFB F013, we collaborate with several national and international groups on geometric inverse problem:

• Department of Mathematics, UCLA
• Laboratoire de Modelisation Mathematique et Numerique, Ecole Nationale d'Ingenieurs de Tunis.
• Institut für Numerische Mathematik und Wissenschaftliches Rechnen, Universität Duisburg-Essen
• Institut für Mathematik, Universität Graz.
• Department of Mathematics, Louisiana State University