Besides Tikhonov regularization, which is probably the most well-known regularization method for linear as well as nonlinear inverse problems, iterative regularization algorithms have more recently been investigated and applied successfully to the solution of, especially nonlinear and large-scale problems. The design and analysis of problem adapted iterative regularization methods is one of the major tasks of this project. Additionally, the efficient implementation, coupling with discretization techniques (forward solvers) and the design of preconditioners are fields of ongoing research.

 

Many iterative methods have been developed and analysed for well-posed problems. Their application to inverse, especially ill-posed problems, is not straight forward and requires an analysis in the framework of regularization methods. There,

• Design and analysis of (new) iterative regularization algorithms:
  in particular Newton-type regularization methods including parameter choice strategies and discretization matters. Recently, a Newton-Kaczmarz iteration has been proposed for the regularization of large-scale problems, especially time dependent problems and parameter estimation from boundary data, where the data is (part of) the Dirichlet-to-Neumann map.
  
  
  • M. Burger, B. Kaltenbacher, Regularizing Newton-Kaczmarz Methods for Nonlinear Ill-Posed Problems, SFB-Report 2004-17. ps-file pdf-file
  • H. Egger, Accelerated Newton-Landweber Iterations for Regularizing Nonlinear Inverse Problems, SFB-Report 2005-3. ps-file pdf-file
  • H. W. Engl, A. Leitão, A Mann iterative regularization method for elliptic Cauchy Problems, Numer. Funct. Anal. and Optimiz., 22(7-8):861-884, 2001. Preprint: ps-file
  • B. Kaltenbacher, A. Neubauer, A. G. Ramm, Convergence rates of the continuous regularized Gauss-Newton method, Journal of Inverse and Ill-posed Problems, 10:261-280, 2002. Preprint: ps-file
  
  
  
• SQP-type methods:
  Such methods are closely related to Augmented Lagrangian or All-at-once methods in optimal control, shape and topology optimization (see also Subproject F1309)). SQP-type methods have been investigated as regularization methods for inverse problems governed by PDE's.
  The main advantage of the SQP approach is that the sparse structure coming from finite element discretizations is preserved in the formulation of the inverse problem. The fast solution of indefinite linear systems naturally appearing in the SQP framework, in particular the design of effective preconditioners, will be the next step.
  
  
  • M. Burger, W. Mühlhuber, Iterative regularization of parameter identification problems by SQP-methods, Inverse Problems, 18:943-970, 2002. Preprint: ps-file
  • M. Burger, W. Mühlhuber, Numerical Approximation of an SQP-type Method for Parameter Identification, SIAM J. Numer. Anal., 40(5):1775-1797, 2002. Preprint: ps-file

One of the major drawbacks of iterative regularization methods for ill-posed problems is that - due to the ill-posedness, which results in ill-conditioned finite dimensional approximations - usually a high number of iterations is needed in order to reconstruct (order optimal) approximations of a solution. This behavior also appears for Newton-type iterations, if the linearized systems are again solved by iterative regularization methods. In order to reduce the overall numerical effort of the solution process, several strategies are pursued:

• Preconditioning iterative regularization methods for linear and nonlinear inverse problems:
  The design of efficient preconditioners has recently become one of the main topics in numerical mathematics, especially in the FEM community. While the theory of preconditioning well-posed problems arising in PDE's is well developed, preconditioning of inverse, in particular ill-posed, problems is not so well understood. Taking into account the ill-posed nature of the problems under consideration, the number of iterations needed to achieve optimal convergence rates for the solution of linear and nonlinear inverse problems by iterative regularization methods can essentially be reduced to the square root by appropriate preconditioning (in Hilbert scales).
  

  
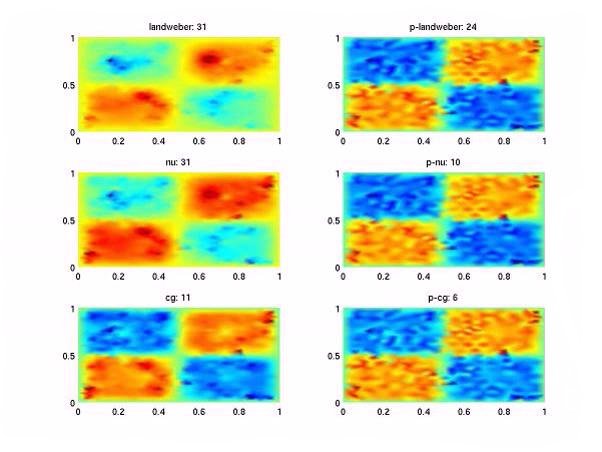
  Reconstruction of an unknown source term.
  Left: standard iterations, right: preconditioned.

  
  
  • H. Egger, A. Neubauer, Preconditioning Landweber Iteration in Hilbert Scales, SFB-Report 2004-25. ps-file pdf-file
  • H. Egger, Semiiterative Regularization in Hilbert Scales, SFB-Report 2004-26. ps-file pdf-file
  
  
  
• Efficient implementation and/or preconditioning the solution of linearized systems arising in Newton-type methods:
  A direct application of Newton's method to the solution of inverse problems is not possible, since the ill-posedness of the nonlinear problem usually implies the ill-posedness of the linearized systems, which have to be solved in every Newton step. In order to ensure stability, the linearized equations have to be solved by regularization methods instead. For large-scale problems, iterative regularization methods turn out to be appropriate. In a first step, acceleration of the Newton-Landweber method by by using faster semiiterative regularization methods for the stable solution of the linearized Newton equations has been investigated. In a second step, the effect of preconditioning will be considered.
  
  
  • H. Egger Accelerated Newton-Landweber iterations for the solution of nonlinear inverse problems, SFB-Report 2005-3. ps-file pdf-file
  
  
  
• Fast iterative solution and preconditioning of indefinite systems arising in SQP methods:
  Saddlepoint problems naturally appear in many applications, e.g., in (Navier-)Stokes equations, or in optimal control problems. Thus fast solution and especially, preconditioning of saddlepoint problems has attracted significant interest in the last years. The saddlepoint problems stemming from an SQP formulation of parameter identification problems governed by PDEs show an additional ill-posedness, i.e., the part of the system, which is usually considered to be uniformly elliptic, now depends on a regularization parameter, which may become arbitrarily small.

The general theory for the regularization of inverse problems is formulated for very general problems. For special classes of problems, the results can be improved significantly. A problem adapted theory of regularization methods, and even the design of problem adapted regularization algorithms is thus an important task. Topics of ongoing research are, e.g.,

• Derivation of a problem adapted convergence theory for selected applications and problem classes.
  
  
  • H. Egger, H. W. Engl, M. V. Klibanov, Global Uniqueness and Hölder Stability for Recovering a Nonlinear Source Term in a Parabolic Equation, Inverse Problems, 21:271-290, 2005. Preprint: ps-file pdf-file
  • H. Egger, H. W. Engl, Tikhonov Regularization Applied to the Inverse Problem of Option Pricing: Convergence Analysis and Rates Inverse Problems, 21, 2005, to appear. Preprint: ps-file pdf-file
  • M. Burger: Iterative Regularization of a Parameter Identification Problem occurring in PolymerCrystallization, SIAM J. Numer. Anal., 39:1029-1055, 2001. Preprint: ps-file
  • H. W. Engl, P. Kügler, The Influence of the Equation Type on Iterative Parameter Identification Problems which are Elliptic or Hyperbolic in the Parameter, Europ. J. Appl. Math., 14:129-163, 2003. Preprint ps-file
  • H. W. Engl, Identification of Parameters in Polymer Crystallization, Semiconductor Models and Elasticity via Iterative Regularization Methods, SFB-Report 2002-02. ps-file pdf-file
  
  
  
• SQP-type methods: As already mentioned, SQP-methods are specially well suited for the application to inverse problems governed by PDE's. Their application to inverse problems for differential inequalities is one of the research topics this project.
  
  
• The design and analysis of new methods, e.g. derivative-free methods, which can be formulated without a derivative of the forward operator or online-algorithms for time dependent inverse problems.
  
  
  • P. Kügler, A Derivative Free Landweber Method for Parameter Identification in Elliptic PDEs, Inverse Problems, 19:1407-1426, 2003. Preprint: ps-file pdf-file
  • P. Kügler, A Derivative Free Landweber Method for Parameter Identification in Elliptic Partial Differential Equations with Application to the Manufacture of Car Windshields, PhD Thesis, Johannes Kepler University, 2003.
  • P. Kügler, An approach to online parameter estimation in nonlinear dynamical systems, SFB-Report 2004-18. ps-file pdf-file
  
  
  
• Level set methods for inverse problems.

Sophisticated discretization strategies become an important factor when it comes to the implementation of regularization algorithms. Especially for large scale problems, the efficient coupling of discretization and iteration process can significantly reduce the overall numerical effort. Topics of recent research are

• Multilevel and multigrid techniques for regularization methods.
  
  
  • M. Burger, W. Mühlhuber, Numerical Approximation of an SQP-type Method for Parameter Identification, SIAM J. Numer. Anal., 40(5):1775-1797, 2002. Preprint: ps-file
  • B. Kaltenbacher, On the regularizing properties of a full multigrid method for ill-posed problems, Inverse Problems, 17:767-788, 2001. Preprint: ps-file
  • Kaltenbacher, B.: A Multi-grid Method with A Priori and A Posteriori Level Choice for the Regularization of Nonlinear Ill-Posed Problems. March 2000. Eds.: Heinz W. Engl, Ulrich Langer ps-file
  
  
  
• Regularization by (adaptive) discretization.
  
  
  • H. Ben Ameur, B. Kaltenbacher, Regularization of parameter estimation by adaptive discretization using refinement and coarsening indicators, Journal of Inverse and Ill-Posed Problems, 10:561-584, 2003. Preprint: ps-file
  • B. Kaltenbacher, Regularization by Projection with A Posteriori Discretization Level Choice for Linear and Nonlinear Ill-Posed Problems. Inverse Problems, 16:1523-1539, 2000. Preprint: ps-file
  • B. Kaltenbacher, A Projection-Regularized Newton Method for Nonlinear Ill-Posed Problems and its Application to Parameter Identification Problems with Finite Element Discretization. November 1998. Eds.: H.W. Engl, U. Langer ps-file
  • B. Kaltenbacher, Regularization by Projection with A Posteriori Discretization Level Choice for Linear and Nonlinear Ill-Posed Problems, Inverse Problems, 16:1523-1539, 2000. Preprint: ps-file
  • B. Kaltenbacher and J. Schöberl, A saddle point variational formulation for projection-regularized parameter identification, Numerische Mathematik, 91:675-697, 2002. Preprint: ps-file
  • B. Kaltenbacher, V-cycle convergence of some multigrid methods for ill-posed problems, Mathematics of Computation, 72:1711-1730, 2003. Preprint: ps-file
  • Kaltenbacher, B.: On a Multigrid Method for Ill-Posed Problems, SFB-Report 1999-20. ps-file

Discretization issues are investigated in close cooperation with Subproject F1306.