Abstract

In this context we have studied neural networks, radial basis functions and Sugeno Controllers (fuzzy control); below we present some results on neural networks.

Learning Theory

Contact: andreas.hofinger@oeaw.ac.at

In this context we have studied neural networks, radial basis functions and Sugeno Controllers (fuzzy control); below we present some results on neural networks.

In a general setup, a neural network can be seen as a parameterized, typically nonlinear, mapping used in function approximation, classification and optimization problems. A popular class of a neural network are so-called feed-forward neural networks with one hidden layer and linear output layer with activation function $\Phi$ , which can be written in the form

$\displaystyle f_k = \sum_{i=1}^k c_i \Phi(x,t_i) .$

(1)

The essential difference to classical discretization methods like splines or finite elements (FE) is that no parameter is chosen a priorily (like e.g. the grid points in FE), but all of them are determined via a nonlinear optimization procedure, the so-called training or learning process. The major advantage of neural networks is their high approximation capability, i.e. for a large class of functions, a dimension independent rate of convergence is attainable. This rate can be achieved only because of the inherent nonlinearity.

Finding optimal parameters of the network can be seen as a nonlinear parameter identification problem, although typically there is no interest in the parameters themselves, but mainly in the output of the network. It turns out that this problem is asymptotically ill-posed, which is not too surprising due to the similarity to parameter identification: small data errors may lead to arbitrarily large errors in the optimal parameters as the number of nodes in the network tends to infinity. In addition, there is also some kind of nonlinear ill-posedness, which is not asymptotic in nature: even networks consisting of only two nodes can lead to instabilities with respect to the parameters in (1) if the nodes get too close. For general, non-smooth (e.g., piecewise linear) activation functions it is also possible to construct examples, where the process is unstable when one is interested in the output measured in higher Sobolev-norms (again even for the case of finite networks).

For these reasons, the training of a neural network has to be regularized. Various regularization techniques have been applied to the ill-posed training process; these methods can be divided into

Tikhonov-type methods and
Iterative regularization techniques

In a first step the regularization methods "weight decay" and "output smoothing" were investigated, and appropriate parameter choice rules have been developed. Although providing stability results and convergence rates these methods do not take care of the underlying structure of the neural network, but consider it just as output of some (highly) nonlinear operator.

Therefore the natural next step is the investigation of iterative methods, like Landweber's method or the Gauß Newton method, which are relatives of the widely used (but unstable!) backpropagation algorithm. The typical nonlinearity or tangential cone conditions which guarantee convergence of these methods are not fulfilled if the network consists of more than one node ("if all neurons learn at the same time"). In order to overcome this problem, a so-called greedy algorithm was developed.

Adaptive Greedy Algorithm

In a greedy algorithm the size of the network is increased successively by only one node each step; the nonlinear optimization process is split into a sequence of low-dimensional problems. Together with an a-posteriori stopping rule, which restricts the final size of the network, convergence of the approximations for the case of noisy data can be shown

Although this approach in principal yields stable approximations, it is not ready for numerical implementation, since it requires unavailable information about the noise-free data (comparable to a bound on the -norm of ).

Therefore an alternative, adaptive method was developed, which is feasible, since the smoothness information above is not needed, but recovered adaptively from the data. Furthermore, the resulting algorithm leads to stable approximations and provides an optimal convergence rate for noiselevel tending to zero.

Open Goals

Inverse Problems: Over the last years, neural networks have also become a frequently used method for solving inverse problems arising in many contexts, from geophysics to medical and economic applications. A sound theoretical basis for using neural networks as algorithms for solving such problems is still missing.
Generalization Error: Neural networks are typically used to approximate functions that are only known at a finite number of sampling points. So far regularization has been investigated for the case of continuous data only, therefore it seems necessary to develop proper modifications of these methods to cover the case of discrete data. An important task in this context is the investigation of the generalization error. This type of error is caused by incomplete or partially missing measurements. In this case instead of the functional 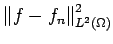$\left\Vert f - f_n\right\Vert^2_{L^2(\Omega)}$ the discrete approximation
$\displaystyle \frac{1}{m}\sum_{i=1}^m \bigl(f(x_i) - f_n(x_i)\bigr)^2$
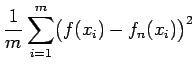
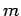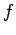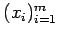is minimized, where measurements of at the points $(x_i)_{i=1}^m$ are given.
Non-smooth Regularization: Another point of interest is the analysis of different (Tikhonov-type) regularization methods, f.i. the maximum entropy method or BV-regularization, which seem more appropriate for the analysis of neural networks with non-smooth activation functions, e.g. the Heaviside function or low order splines.
Network Architecture:: An overall question to answer is the choice of the optimal network architecture. So far, we derived methods for determining the optimal size of single layer networks (corresponding to the stopping index of the greedy algorithm). As a next step, also multilayer networks can be considered. It is not obvious if methods such as the greedy algorithm can be transferred to these more complex structures.

U. Bodenhofer, M. Burger, H. W. Engl, J. Haslinger, Regularized data-driven construction of fuzzy controller, Journal of Inverse and Ill-posed Problems, 10 (2002), pp. 319-344. Preprint: .pdf, .ps.gz
M. Burger H. W. Engl, Training neural networks with noisy data as an ill-posed problem, Advances in Computational Mathematics, 13 (2000), pp. 335-354. Preprint: .ps.gz
M. Burger, A. Hofinger, Regularized greedy algorithms for network training with data noise, Computing, to appear (2004). Preprint: .pdf, .ps.gz
M. Burger, A. Neubauer, Analysis of Tikhonov regularization for function approximation by neural networks, Neural Networks, 16 (2003). Preprint: .ps.gz
M. Burger, A. Neubauer, Error bounds for approximation with neural networks, Journal of Approximation Theory, v.112 n.2 (2001), pp. 235-250. Preprint: .ps.gz
A. Hofinger, Iterative regularization and training of neural networks, Diplomarbeit, Johannes Kepler University Linz, 2003. Preprint: .pdf.gz
A. Hofinger, Nonlinear function approximation: Computing smooth solutions with an adaptive greedy algorithm, SFB Report 04-19, Johannes Kepler University Linz, SFB "Numerical and Symbolic Scientific Computing", 2004. Preprint: .pdf, .ps.gz

Uncertainty

Contact: andreas.hofinger@oeaw.ac.at

Another aspect which we want to address is "uncertainty", which is currently a hot topic in connection with inverse problems especially in the U.S. While we (and most of the functional analysis based inverse problems community) treat the error in the data (and also in the model) via a bound on some function space norm, there, a different, i.e., stochastic, error concept, is used. Convergence then cannot be studied by giving error estimates in some norm, but one has to consider different convergence concepts for random variables.

One standard approach here is to replace convergence of deterministic quantities,by convergence of the root mean square error RMSE.

We consider a different approach, where instead of convergence of random variables, the convergence of the underlying probability distributions is investigated. The proper tool for metrizing the convergence of probability distributions is the Prokhorov-metric.

One advantage of this approach is that the deterministic results are contained in the new theory, since deterministic quantities correspond to the delta-distribution and $\rho(\mu_{\delta_x},\mu_{\delta_y})=\left\Vert x-y\right\Vert$ , i.e., delta-distributions converge with the same speed as the underlying variables. Another important feature is that infinite-dimensional problems can be easily considered, whereas in stochastic approaches the model must typically be discrete to allow for analysis.

So far Tikhonov-regularization for linear equations in a fully stochastic setting has been investigated, and results for convergence and convergence rates have been obtained. The results are derived for a very general setup that is applicable to a wide variety of (linear) stochastic ill-posed problems. These contain for instance the following cases

Deterministic equation with random error
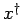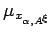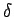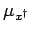Since the data is modelled as random variable, also the (pointwise) regularized solution is a random variable. Consequently, convergence of regularized solutions to the least squares solution $x^\dagger$ in the deterministic setting, now translates to the convergence of a distribution $\mu_{x_{\alpha,A^\xi }}$ to the $\delta$ - distribution $\mu_{x^\dagger}$ .
Stochastic operator is approximated by operator 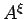which is
- fixed deterministic
- fixed deterministic with overlaid stochastic noise
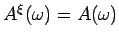- stochastic and noise-free (i.e., $A^\xi (\omega)=A(\omega)$ )
- stochastic with overlaid noise
Combination of these

A key step in the new approach is the lifting of a locally Lipschitz continuous map to the space of probability measures, which allows to transfer existing deterministic estimates to a stochastic setting.

H. W. Engl, A. Walkolbinger, Continuity properties of the extension of a locally Lipschitz continuous map to the space of probability measures, Monatshefte f. Math. 100 (1985), 85-103.
H. W. Engl, A. Hofinger, S. Kindermann, Convergence rates in the Prokhorov metric for assesing uncertainty in ill-posed problems, Inverse Problems, 21:399-412, 2005. Preprint: .pdf, .ps.gz

Please direct your comments or eventual problem reports to webmaster.

SpezialForschungsBereich SFB F013 | Special Research Program of the FWF - Austrian Science Fund