The weak formulation

The partial differential equation describing a heat flow problem with thermic conductivity $\lambda$, a volumetric source density $f$, an inflow density $g$ at the part $\Gamma_N$ of the boundary, and a heat exchange to the environment of temperature $u_0$, and conductivity $\alpha$ on $\Gamma_R$ is

$$\begin{array}{rcll} -\mbox {div} \lambda \nabla u & = & f \q... ...& = & \alpha (u_0 - u) \quad & \mbox{on } \Gamma_R. \end{array}$$

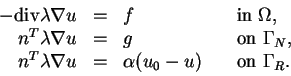
The weak form of the equation is to find the temperature distribution $u$ in the proper Sobolev space $V := H^1(\Omega)$ such that

$$\int_\Omega \lambda \nabla u \cdot \nabla v dx + \int_{\Gamm... ...\int_{\Gamma_N} g v ds + \int_{\Gamma_R} \alpha u_0 v ds$$

holds for all test functions $v \in V$. The finite element method replaces the Sobolev spaces $V$ by a finite dimensional sub-space.

The PDE input file defines the variational problem. You specify the finite element space, and then, the bilinear-form (left hand side), and the linear form (right hand side) are build up from elementary blocks called integrators. The table below lists the names of the integrators needed in the equation above:

laplace lam	$\int_\Omega \lambda \nabla u \cdot \nabla v dx$
robin alpha	$\int_{\Gamma_R} \alpha u v ds$
source f	$\int_\Omega f v dx$
neumann g	$\int_{\Gamma_N} g v ds$

Note that the last term is handled by the neumann - integrator with coefficient $\alpha u_0$. You might miss Dirichlet boundary conditions. Indeed, NGSolve always approximates them by Robin b.c. with large conductivity $\alpha$.